Return to
My Adventures in Asia
My wife introduced me to a popular game played in Indonesia, Malaysia and the Philippines
called
Congklak.
It has many other names including Congkak, Dakon and Sungka.
Wikipedia has a good description of it.
This page lists the history of the game and
says there are 279 known names for the game. The number of holes and pieces per hole can vary
but the game is the same. The most common setup is 7 holes with 7 pieces per hole.
Here are some pics of other boards:
1
2
3
4
5
I've seen them with as little as 5 holes per player and up to 10 holes per player.
I'm sure the pieces per hole also vary but regardless of holes and pieces the game is still the same.
I was frustrated at first because Kelly was so much better than me and I hate to lose
so we kept playing and over time I got better and better.
I noticed that she had a very good
opening move which gave her a great lead improving her chances of winning.
Instead of just copying her opening move, I decided to find my own better move.
So I wrote a C++ program to find the best possible opening move.
You can get the source code
here.
The main part of the program contains 99 nested loops.
To make sure that I had no typos in my code I wrote another program that generated
this repetitive code for me so I know it is perfect.
It generated about 300 lines of code for me.
The PC-based executable is
here.
Unzip the exe into any directory and run from the command prompt to get the syntax and
instructions.
The results were far greater than I expected.
I was looking for an opening move to improve my chance of winning but what I found instead is an
opening move that insured my win. In other words, if I go first, I always win.
Now that I have unlocked the secret opening moves, I can no longer go first when we play.
My program can calculate the best moves for any given board so even if I go second, I will still always win.
In other words, using my program is totally unfair. I could give the other player nearly half
of the pieces and my program would probably still find a way to win.
To confirm that my program was generating valid output I test played it using
this
PC DOS version.

Assuming you are playing on the board shown above and your holes are 1 thru 7 and your pocket is 8,
the best opening move I have found is 1252151. This means that you pick up the pieces in hole 1 and play them
until the last piece ends in your pocket. Repeat for holes 2, 5, 2, 1, 5 and 1. Then your turn will
be over and you will have accumulated 46 pieces in your pocket on the first move!
There are 98 pieces total so this would leave 52 pieces left.
All you need is 50 pieces to win since that is one more than half.
Even if you tried to lose, you'd still win.
If you want to make it official and take exactly 50 pieces and win the game on the first move
then you can do it in 11 moves. There are 8 different ways to take 50 pieces in 11 moves.
- 12521522366
- 12521522464
- 12771351211
- 17416431764
- 17416434452
- 17416434657
- 17416772347
- 17557514663
Note that the first two solutions are the 7 move solution 1252151 that gets you 46 pieces
except the last number is 2.
Using these 9 moves, 127713147, you can get 54 pieces. Sometimes less moves gets you more pieces!
If you really want to impress your opponent you can take 96 of the 98 pieces on the first move with these 71 moves.
17753575677576737571757346576737176727547747637725756547761767374717375
Oh sure, you can do it less moves but the longer your turn lasts, the more impressed they'll be!
If you just want to get the job done in the shortest time, here is a way to do it in 39 moves
125215272716242447567163777367473747671
So far I have not been able to find a solution that gets you 97 or 98 pieces.
It may not exist but if you would like to help then contact me at
patcoston@gmail.com.
Here are some other things I'm searching for. Please contact me if you'd like to help!
- Moves to get most pieces in a hole at any point
- Moves to get most pieces in a hole at end of a turn
- Moves to get most pieces in a hole at end of a turn which can be taken by opponent
- Most number of holes visited on a single turn (round trips around the board)
If you want to make exactly a certain number of moves then try these links which
list all possible solutions for that number of moves:
1
2
3
4
5
6
7
8
9
10
I would have posted more but the text files were getting way too big!
Interesting notes: If your first move is any other than position 1 then you'll just have one move
resulting in exactly 10 pieces captured. If you only want to memorize 3 moves then remember 132 which will get
you 28 pieces. 1271 is the best 4 moves getting you 39 pieces. 17412 is the best 5 moves getting you 38 pieces.
It is strange how 5 moves gets you less than 4 moves. 127715 is the best 6 moves getting you 35 pieces.
1252151 is the best 7 moves getting you 46 pieces.
Fun Puzzle
Start with 1 piece in each of your 7 holes and move all 7 pieces into your pocket.

Try to solve this puzzle in the shortest number of moves.
Hints:
- Never have two pieces in hole 7
- Always try to move the most number of pieces with each move
The solution is shown below using this board numbering.

There are two solutions: 71734757 and 71737457
Next try finding the longest solution.
Hints:
- The longest solution is 28 moves
- There are millions of this worst-case solution
- Never have two pieces in any hole
The two most obvious solutions are 7654321765432765437654765767 and 7675674567345672345671234567
which happen to be opposites of each other.
Hard Puzzle
Setup your board as shown below: 1, 2, 3, 4, 5, 6 and 7 pieces in the holes with your pocket on the left.
This is the most number of pieces you can finish the game on your turn with. As long as you don't put any
pieces on your opponents' side, you can keep moving them into your pocket.
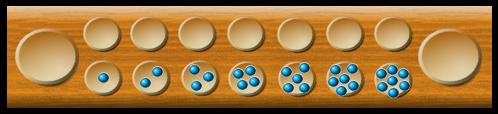
Try to get all 28 pieces in your pocket in 29 moves.
If you give up, the 6 possible solutions are shown below.
- 76757476737276757671727475767
- 76757476737476727571727475767
- 76757476737576727571727475767
- 76757476737672757671727475767
- 76757674737672757671727475767
- 76757674757375727571727475767
Notice that the piece in hole 7 gets moved every other move.